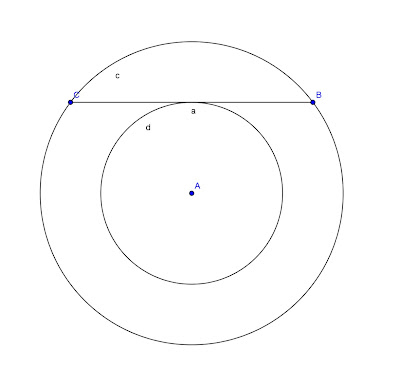
El problema consiste en hallar el area de la corona circular conformada por ambas circunferencias concentricas conociendo la longitud del segmento BC, tangente a la circunferencia de menor radio (Adjunto el grafico para facilitar la interpretacion geometrica)
GRADO DE DIFICULTAD: 1 La semana que viene se publicara la solucion al mismo
SOLUCION= La solucion es casi trivial basta considerar d=BC/2 es decir desde el punto de tangencia a B por otro lado tenemos los radios R y r R=AB y r=AT siendo T el punto de tangencia, claro que el triangulo conformado por AB,AT y BC/2 es rectangulo aplicamos el teorema de pitagoras en lo sucesivo, pero A corona=pi*R^2-pi*r^2 =pi(R^2-r^2)=pi(AB^2-AT^2) , pero aplicando la relacion pitagorica se tiene que AB^2=AT^2+(BC/2)^2, en particular AB^2-AT^2=(BC/2)^2 sustituyendo en la expresion anterior tenemos el resultado A corona=pi*(BC/2)^2 q.e.d.

2 comentarios:
y para cuando tienes la respuestaa??
ahi la tienes siento la tardanza!
Publicar un comentario